結城浩の「コミュニケーションの心がけ」2017年4月4日 Vol.262
はじめに
おはようございます。結城浩です。
いつも結城メルマガをご愛読ありがとうございます。
もう四月ですね。
待望の春です!
関東はあちこちで桜が見られるようになりました。 今週が見頃なんでしょうか。
新年度、 新しい場所でスタートを切った方も多いでしょうね。 あなたのスタートはいかがですか。
結城は今年に入ってから、 家庭の事情で何かと気ぜわしく、 仕事に十分な時間を注げない日々が続いています。 なかなかつらいです。
でも、今年は晴れた日が多くて、 それだけでも気分はすこしよくなりますね。
新刊となる『数学ガールの秘密ノート/積分を見つめて』 の執筆もがんばっています。
微分が瞬間の変化をとらえたものだとすれば、 積分は変化を集めていったものともいえます。
季節の変化も、気分の変化も、 生きている証拠。
生きているからこそ変化に出会い、 変化を感じ取ることができるのです。
新しく巡ってきた春という季節を、 ていねいに過ごしていきましょう!
* * *
十年目の話。
先日、編集部より、
『数学ガール』が増刷になる
という連絡が入りました。感謝です!
今回の増刷で28刷。初版が刊行されたのが2007年ですので、 今年で丸十年になりますね。 読者さんが継続的に応援してくださること、 心から感謝しています!
◆「数学ガール」シリーズ
http://www.hyuki.com/girl/
* * *
黄金比の話。
John D. Cookのブログで「黄金比φの冪乗は整数に非常に近い」 という話題が書かれていました。
◆Golden powers are nearly integers
https://www.johndcook.com/blog/2017/03/22/golden-powers-are-nearly-integers/
黄金比φは、フィボナッチ数1,1,2,3,5,...の比の極限値に等しく、 具体的には(1+√5)/2=1.61803...という値です。 この黄金比の2乗、3乗、4乗、……を計算していくと、 非常に整数に近くなるというのです。
上のブログでは、ちょっとしたコードを書いて確かめていました。 結城も同じようにちょっとしたコードを書いて確かめたくなりました。 以下にRubyで書いたコードがあります。
◆φ^n looks like an integer.
https://gist.github.com/hyuki0000/2e33150caa99195330a817fb07d98472
◆φ^n looks like an integer(スクリーンショット)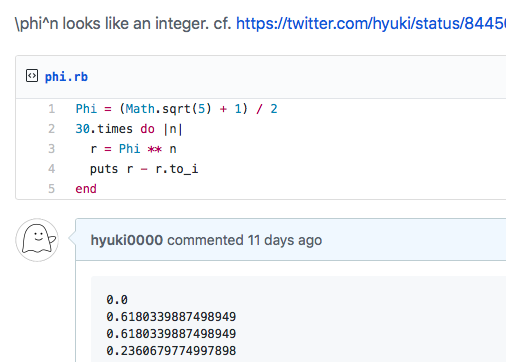
このコードでは「黄金比を冪乗した値」と「その値を切り捨てた値」 との差を計算しています。すると……
0.0
0.6180339887498949
0.6180339887498949
0.2360679774997898
0.8541019662496856
0.09016994374947629
0.9442719099991628
0.03444185374863906
0.9787137637478054
0.013155617496451555
0.9918693812442569
0.005024998740708497
0.9968943799850081
0.0019193787256881478
0.9988137587107531
0.0007331374365548982
...
のように、 どんどん0または1に近づいていくのがわかります。 とても興味深いことです。
そして自分で「ちょっとしたコード」を書いて試すというのは、 自分の印象に強く残るということも実感しました。
わずか5行のコードですけれど、 これを書くためには、 「黄金比の冪乗は整数に近い」という文章を理解し、 それをプログラミング言語で表現する必要があります。 そのプロセスを通り抜けることによって、 強く印象付けられるのかもしれませんね。
* * *
ネット時代を心穏やかに過ごす話。
Twitterでいろんな人のツイートをながめていると、 ときどき、
・自分の考えにまっこうから反対の意見を述べるツイート
・自分が大事にしているものを非難するツイート
を見かけることがあります。
当然ながら、 そのようなツイートを読むと心は穏やかではありません。 つい、その意見にリプライしたり、反論を試みたくなります。 そんな経験はありませんか。
結城は、他人のツイートを読むときに、
……と、この人はツイートしている。
あるいは、
……と、この人は考えている。
などをツイートに付加して読むように心がけています。 そのようにすると、 心穏やかに過ごせるケースが多いのです。
たとえば、
「○○はまちがっている!絶対に△△だ!」
というツイートを見かけたときには、
「○○はまちがっている!絶対に△△だ!」
……と、この人はツイートしている。
と読み替えるのです。
あるいはまた、
「作家の□□が書いた小説はつまらんな!」
というツイートを見かけたときには、
「作家の□□が書いた小説はつまらんな!」
……と、この人は考えている。
と読み替えるのです。
読んだときの印象がずいぶん変わりますよね。
ツイートを通して、言葉は目に飛び込んできます。するとつい、 その言葉を額面通りに受け取ってしまいそうになります。 言葉には力があるからです。
でも、実際は、ある特定個人のツイートにすぎませんし、 その人の個人的な考えの表明にすぎません。
「 」……と、この人はツイートしている。
「 」……と、この人は考えている。
そのようにワンクッション置くことで、 違った景色が見えてくるものです。
ネット時代を心穏やかに過ごすために、 ぜひ、試してみてください。
……と、結城は考えています。
* * *
報道機関の話。
上に書いたのはTwitterのことですが、 報道機関についても同じような感覚は必要かもしれません。
フェイク・ニュースとまでは行かなくても、 どんな報道機関も何かしらのバイアスは掛かっているものです。 ですから、ニュースを見聞きしたときにはニュース・ソースを確認して、
「 」……と、○○新聞は考えている。
「 」……と、○○テレビ局は考えている。
のように判断する必要はあるでしょうね。
「社会を変えたい」と考える報道機関よりも、
「自分たちの考えに反することでも事実は事実として伝える」
と考える報道機関の方が社会を変える。
結城はそのように考えています。また、
「私たちは間違わない」と考える報道機関よりも、
「私たちは間違う。間違いは認めて訂正する」
と考える報道機関の方が信用できる。
とも思います。
報道機関が「社会を変えたい」と考えすぎると、 そのような考えに合致するニュースを強く報道し、 その考えに反するニュースを軽んじる危険性があります。 それこそがバイアスになります。
報道機関が「私たちは間違わない」と考えると、 誤った報道をしてしまった場合の訂正が遅れる危険性があります。
バイアスがまったく存在しない報道機関はありえないでしょう。 しかし、報道機関には科学的な態度が必要です。
ここでいう科学的な態度というのは、 「現在の自分の考えが正しいとは限らない」というほどの意味です。
自分の考えが正しいとは限らないという認識に立つと、 何かを報道するときでも注意深くなるでしょう。 自社の考えを補強するようなニュースだけを報じるのではなく、 社会のようすをできるだけ正確に報じる姿勢になるでしょう。
これに関連して、 メダワーの書籍『若き科学者へ』も思い出しました。
--------
ある仮説を真であると信じる気持の強さは、
それが真であるか否かには何の関係もない。
--------
◆『若き科学者へ【新版】』(ピーター・B・メダワー)
https://www.amazon.co.jp/exec/obidos/ASIN/4622085305/hyuki-22/
おりしも新学期。高校生・大学生に、 この『若き科学者へ』を強くお勧めいたします (結城は本書新版の巻末解説を書きました)。
* * *
発想をうながす話。
結城は「発想をうながす」ことに関心があります。 それは、ふだん一人で仕事をしていることが多いからかもしれません。
一人で仕事をしていると、 自分のふだんの発想だけで考えを進めてしまいがち。 そうすると話は広がらないし、新しいものを生み出すのは難しい。 ということで「発想をうながす」ことに関心があるのです。
Twitterを見るのが好きなのも、それに関係がありそうです。 他人のつぶやきを眺めていると、そこで提示されている話題について、 つい考えてしまいます。他の人がツイートしていることなので、 ふだん自分が考えないような話題が出てきたりします。 それは確かに、自分の「発想をうながす」ことにつながっています。 職場で同僚とおしゃべりする感覚に近いかもしれませんね。
以前、こんなサービスを考えたことがあります。 自分が持っている本(PDF化された本)の、 ランダムなページを自分にちらっと見せるというサービス。 もちろん、著作権の問題があるので、 パブリックなサービスにはできませんし、 結局実装もしませんでした。
自分が持っている本は、自分が関心のある話題について書かれています。 ですから、その中身を「チラ見せ」することで、 自分の頭に刺激を与えることができるんじゃないかな、 と思ったのです。
「チラ見せ」サービスは、 体系的に学ぶには不向きですけれど、 「理解のブレークスルー」を起こす効果があるように思います。
学生時代なのでずいぶん昔の話になりますが、 アルゴリズムについて友人とおしゃべりしていたことがあります。 O(n)やO(log n)のようなアルゴリズムの「オーダー」 について私はまだ理解していませんでした。
でも、友人が、 「アルゴリズムに掛かる手間はデータサイズnに依存するよね」 と一言いった瞬間に、 「なるほど!そういう概念なのか!」 と深く理解した経験があります。
そのとき、概念を理解するための素材は頭の中に蓄えられていました。 その状態で、友人からの一言が刺激となって、 「理解のブレークスルー」を引き起こしたのですね。 あの体験は忘れがたいものでした。
順序を追って学ぶのは大事なことです。でもそれとは別に、 友人の一言や、ちらっと見かけたツイートを通して、 頭の中で何かが発火して「理解のブレークスルー」を起こす。 そして、新しい発想がうながされる。 そのようなプロセスも、学ぶ上で大事じゃないかなと思うんです。
ものごとの理解は、一直線に進むとは限らないからです。
* * *
とってもかわいいissueの話。
Githubは、ソフトウェアを開発するWebサービスのひとつです。 多くのプログラマが日々ソースコードを公開したり、 バグ報告をしたりとGithubを使っています。
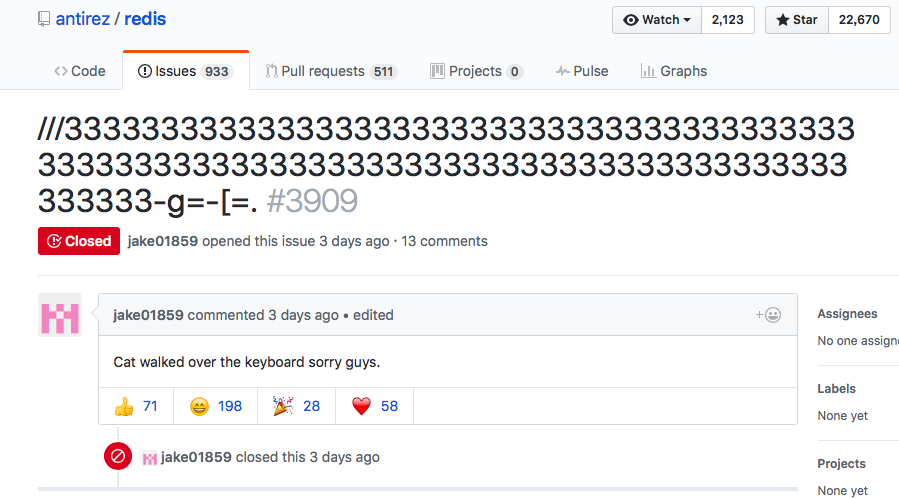
先日、とってもかわいいissueの話題を知りました。 バグや質問などを報告するissueとして、 このような謎の書き込みがあったのです。
--------
///333333333333333333333333333
333333333333333333333333333333
33333333333333333333333333333333-g=-[=
--------
まるで暗号ですね。そしてその直後、 この投稿を行ったjake01859氏が、こう書き込みました。
--------
Cat walked over the keyboard sorry guys.
(猫がキーボードの上、歩いたんだよ。ゴメン、みんな)
--------
猫がキーボードを歩いたために、 謎のissueが投稿されてしまったのですね。
猫の様子を想像して、たいへん和みました!
それに続く開発者たちのコメントも、 駄洒落を書いたり、猫の歩いたようすを解析したり、 猫がいないから再現できないといったり…… たいへん楽しいものでした。
◆猫のissue
https://github.com/antirez/redis/issues/3909
* * *
では、そんなところで、 今回の結城メルマガを始めましょう。
どうぞ、ごゆっくりお読みください!
目次
- はじめに
- 外部要因を制御する - 仕事の心がけ
- 《問いかけ》が持つ危険性
- 執筆が進まないのには理由がある - 本を書く心がけ
- またね!
- おわりに







コメント
コメントを書く