今回はやねうらおさんのブログ『やねうらお－俺のブログがこんなによっちゃんイカなわけがない』からご寄稿いただきました。

■古くて新しい自動迷路生成アルゴリズム

最近、ゲーム界隈ではプロシージャルテクスチャー生成だとか、プロシージャルマップ生成だとか、手続き的にゲーム上で必要なデータを生成してしまおうというのが流行りであるが、その起源はどこにあるのだろうか。

メガデモでは初期のころから少ないデータでなるべくど派手な演出をするためにプロシージャルな生成は活用されてきたが、ゲームの世界でプロシージャル生成が初めて導入されたのは、もしかするとドルアーガの塔(1984年/ナムコ)の迷路の自動生成かも知れない。

なぜ私が迷路のことを突然思い出したのかと言うと、最近、Twitterで「30年前、父が7年と数ヶ月の歳月をかけて描いたA1サイズの迷路を、誰かゴールさせませんか。」というツイートが話題になっていたからである。

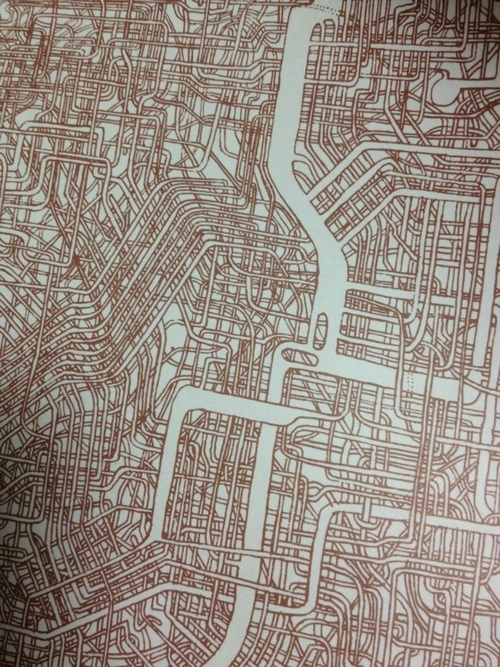
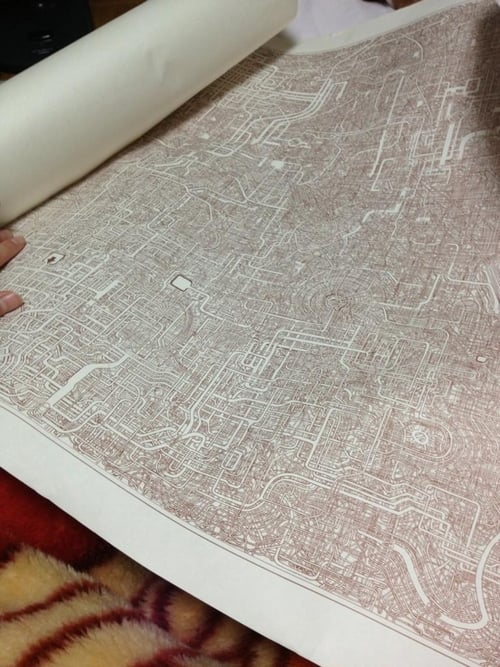
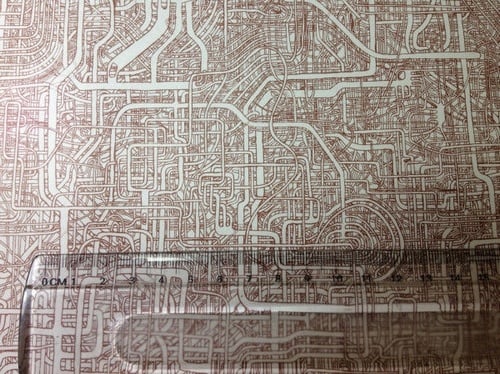
この迷路を見て「ああ、俺様も迷路のことを書かねば！俺様しか知らない(?)自動迷路生成のことを後世に書き残さねば！」と誰も求めちゃいない使命感がふつふつと湧いてきて、明日は大事なプレゼンがあるというのにかなりの長文になるであろうこの記事を書きだしたわけである。読者諸氏におかれましては「ああ、またいつもの病気か」とぐらいに思っておいていただきたい。

余談ではあるが大事なことなのでいま書いておくとだな、年が明けてからと言うもの、私が書く記事、書く記事にたくさんはてブをしていただき、たくさんのPVがあったのは本当にブロガー冥利に尽きるというものなのだが、アマゾンの商品の紹介をほとんどしていないものでアマゾンのアフィリ料はほとんど入ってこない。昨年のアフィリ収入は数年前と比較すると1/10のすらない。

写真提供『女装する人がひたすら脱毛について語るブログ ゆきにゃん』

http://yukinyan.info/

「うわっ…私のアフィリ料、低すぎ…？」

ほれ見ろ！鹿目まどかさんもアフィリ料があまりに少なすぎておもわずオシッコちびってしまったではないか！(えっ。これオシッコじゃないの？)

冗談はさておき。

ドルアーガの塔で迷路を自動生成しているのは「プロシージャルに生成して、遊ぶたびにライブ感を！」という試みではなく、単にROM容量が少なく、マップのための容量が惜しかったからである。(生成されるマップは毎回同じである。)

「容量が惜しい」とは言っても、下図のように柱と柱の間の壁の有無だけなので1フロアにつき垂直方向の壁17*9 + 水平方向の壁18*8 = 153 + 144 = 297ビット。これが60フロア分で17820ビットすなわち2223バイトあれば収まる。

ドルアーガの塔 アーケード Floor1

ドルアーガの塔のROMは32KB×2だったように思う。これはマッピーの基板が2000枚ほど余っていて、それを流用するためにドルアーガの塔を作ったので、マッピーのときの仕様を引きずっているのだと思われる。2223バイトが本当に惜しかったのかどうかは私にはよくわからない。

そもそもマップをよーく見ると、柱から上下左右のいずれか一方向に柱が倒れたかのように壁が存在するので倒れた方向2ビット×柱の数でよく、上記の半分ぐらいで収まる。そう考えると本当に1KB強のメモリが惜しかったのだろうか…という疑問がなくはないのだが。

さて、ドルアーガの塔のようなゲームの迷路を自動生成する場合、良い迷路とはどのような迷路だろうか？

「良い迷路」を言葉で定義するのは難しいが、明らかにまずい例を一つ挙げることは出来る。

壁の閉ループ(袋小路)はまずい。ダメ絶対！

ドルアーガの塔では壁を壊すためのアイテム(マトック)をゲーム開始時には主人公が持っていないので、袋小路に主人公が出現すると詰んでしまう。

あと、迷路はある程度入り組んでいないといけない。鍵と扉の出現位置はランダム(だと思う)が、宝箱は主人公の開始位置に出現する。宝箱の出現条件を満たし、宝箱を回収して、鍵を取って扉に入るわけだが、これらの移動距離があまりに短いとゲームとしてつまらない。

この入り組み加減を実現するために、通路がループになっているものを禁止する。ここではそのようなループのことを「開ループ」と呼ぶことにしよう。開ループがあると、ある地点からある地点への経路が複数できてしまうので入り組み度が下がる。開ループを禁止すれば、ある地点からある地点への最短経路は一意に定まる。ゆえに、解(開始位置から扉への経路)の唯一性も保証される。

入り組み度を上げるための方法は他にもいろいろあるが、専門的になりすぎるので割愛する。

あと、迷路がワンパターンではないこと。これも重要なファクターである。左上が入り口で右下が出口であるとき、どの迷路も真ん中あたりを通過する経路を選べばゴールできるだとか、特徴が似通っているのはよろしくない。

ともかく、そのような視点で見たときに、上図のマップは非常によく出来ている。入り組み方とかが芸術的とも言える。

ドルアーガの塔の画面はマッピーと同じく横スクロール型なのでマップ全体がプレイヤーに見えているわけではない。ある程度スクロールさせないと鍵や扉の位置がわからず、鍵を拾ってから扉に移動するまでに壁を壊せないなら、かなり回りこまないといけないことも多い。このへん、ゲームとしてうまく出来ている。

このようなマップはどのようにすれば生成できるだろうか？というのを考える前段階として、迷路の自動生成に関する一般的な手法をいくつか紹介する。

私の記憶によると、創刊号付近のマイコンBASICマガジン(30年前か…)にBASICで書かれたPC-8001用の迷路自動作成プログラムが載っていたと思う。小学生だった私はそれをせっせとPC-6001用に移植して走らせたのを覚えている。

そのアルゴリズムは確か、いわゆる穴掘り法と呼ばれるもので、画面上のランダムな位置から開始して、適当に掘り進み(2コ先が通路でないなら掘る)、現在地点の四方向とも掘り進めなくなれば(2コ先×4方向がすべて通路なら)、いままで掘ってきたところを一つずつ戻っていき(掘った経路は覚えている)、そこからまた掘っていくというアルゴリズムである。

『迷路自動生成アルゴリズム』

http://www5d.biglobe.ne.jp/%257estssk/maze/make.html

３．穴掘り法（道延ばし法）

穴掘り法（道延ばし法）は、最初面全体を壁にします。道延ばしの際に、迷路の外に道を延ばすのを防止するテクニック(判定を高速化する方法)として、最外周をあえて道にしておくテクニックもよく使われます。

穴掘り法の基本は、ランダムに点を選んで、そこから延ばせる限り道を伸ばしていきます。上下左右のいずれかの方向に２マス先を見て、そこが通路でなければ道を延ばします。道を延ばす事ができなくなれば、この時既にある道からランダムに点(但し、Ｘ座標とＹ座標が偶数の点)を選んで道を延ばします。

これを繰り返すして、画面全体を道で埋めたら完成です。棒倒し法よりも人が迷路を書く方法に近いため、道のランダム度は高くなります。

行き止まりになるまで道を生成するというアルゴリズムの特性があるので、道の行き止まりがあると、その周囲の道はそれより先に生成されているはずです。この事からプログラムがどのような順序で通路を生成したか、ある程度予想できてしまいます。

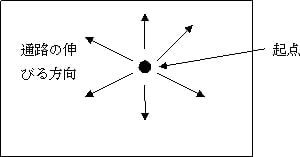
この迷路の生成方法は、大きく見ると、起点を中心に放射状に通路を発生させる傾向があります。つまり、スタートから、迷路生成の基点付近を通り、ゴールへ向かう道が答になりやすい傾向があります。小さな迷路では気になるになりませんが、大きな迷路を生成した場合に、解答が単調になります。また通路がランダム曲がり、直線が少ないので、大きな迷路を生成した場合、見た目はゴチャゴチャした感じになります。

穴掘り法は入り組んだ迷路が生成されるのだが、開始点から放射状の迷路が出来るので、大きな迷路だとあまり評判はよろしくない。

穴掘り法以外のアルゴリズムとして棒倒し法、壁のばし法などがある。(上の『迷路自動生成アルゴリズム』URLを参考に)

それらは出来がいまひとつなのでここでは紹介しない。

それらとは一線を画すアルゴリズムとしてクラスタリングアルゴリズムというのがある。

「クラスタリングによる迷路作成アルゴリズム」 『渡辺宙志 / WATANABE Hiroshi』サイト

http://apollon.issp.u-tokyo.ac.jp/~watanabe/tips/maze.html

迷路の作成アルゴリズムは以下の通り。
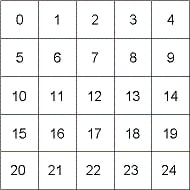
・部屋を要素とし、通し番号をつけておく

・ランダムに壁を壊す。このとき、隣あう部屋がつながったとしてクラスタリングする

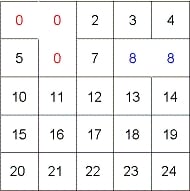
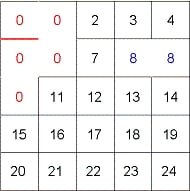
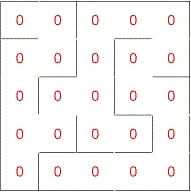
・同じクラスタ番号に属す部屋の間の壁(下図の赤い線)は壊さない (ループを作らない保証)。

・すべてが同じクラスタ番号に属すまで続ける(死に領域が出来ない保証)

以上で死に領域とループがない迷路の完成である。

以上のアルゴリズムを用いて、「解くと絵が浮かび上がる迷路」を 作ることができる。やり方は簡単で、先に解答のパスを作り、その部分だけ クラスタリングしてから壁を壊し始めれば、ループを作らない保証から与えた解答が最短距離となる迷路が出来上がる。以下の図はそのようにして作成した迷路の例である。 左図の迷路を解くと、右図のような絵が浮かび上がる。

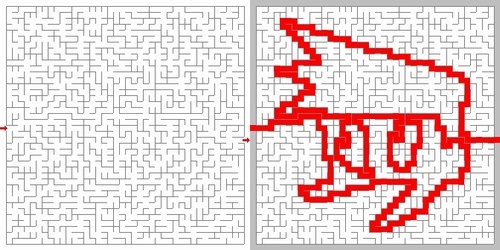
クラスタリングと言ってもPCを複数台用意して…みたいな話とは全く違って、単に部屋に番号をつけておき、壁を壊すときに同じ番号(同じ仲間)にするというアルゴリズムである。

このアルゴリズムは実に明快で、実装しやすい。また、開ループ・閉ループが作られないということの証明が容易で、教育的にも好ましい。

ただ、それぞれの壁に対して乱数によって一定確率で壊していいか(その壁に隣り合うのは異なる部屋番号か)を判定することを繰り返すようなアルゴリズムになっているので、大きな迷路だとなかなか最後のほうの壁が壊れなくて時間がかかるかも知れない。(まだ壊していない壁だけを配列に持っておき、そこだけを調べればもう少し効率的だが…。)

あと、迷路の入り組み加減はどうなんでしょう…。壊していい壁がランダムに壊されていくようなモデルなので、比較的癖のない迷路になるんですかね。

以上のことを踏まえた上で、ドルアーガの塔の迷路生成アルゴリズムに踏み込んでいく。

「『ドルアーガの塔』編」 『D/LAB――『ドルアーガの塔』研究室』

http://www.druaga.to/qanda_tod.html

TODの迷路は、まず全ての柱を想定します。そして、最初の１本を選び、そこから面数を根とした乱数によって、０～３の数を導き出し、それに相当する方向（ex.０:上、１:右、２:下、３:左）に壁を作ります。それが外壁か別の壁に接触しなければ、新しい根より０～２の乱数をもとめ、そちら方向（ex.０:進行方向左、１:まっすぐ、２:進行方向右）へ壁を伸ばします。これを外壁か別の壁に接触するまで続けます。

もし外壁か別の壁に接触した場合、最初に選んだ柱から順番に、まだ壁の通過していない柱を選んで同じ処理を繰り返します。壁の通過していない柱がなくなると迷路の完成、結果として、迷路のある地点Ａから別の地点Ｂまで１通りしかルートのない、狭義の意味での迷路ができるのです。

このフロアを元にした乱数の根を255にすると、なぜか整然とした迷路になってしまったので、これを特別に最上階60階の迷路用の根として、残りはフロア数がそのまま迷路のデータとなっているのです。

あのフロア全てをデータで持つと大変なのですが、このような方式で作成しているため、全く同じ方法を取ったとしても、迷路のサイズが異なれば構造が違ってしまうわけです。遠藤としては、最上階以外のフロアの形状に関しては、まったく関心がなかったので、移植が同じ方法で迷路を生成しているのは、かえって新鮮で良いのでは？と思いました。

◇　これはおもしろい発想ですよね。CD-ROM・DVD-ROM全盛の今からは想像もつかないようなデータ圧縮の苦労が、当時にはあったわけです。

--------------------------------

□　ちょいと気になったのですが、そのアルゴリズムでは「ドルアーガ」の迷路を生成することは出来ないのでは？

具体的に説明すると、

　　１．迷路の中央あたりの柱から上方に壁が伸びる。

　　　　↓

　　２．上の外壁に触れる。

　　　　↓

　　３．最初の柱から下方に壁が伸びる。

　　　　↓

　　４．下の外壁に触れる。

とステップが進んだ場合、左右に分断された迷路になってしまいます。

また、このアルゴリズムでは生成される壁はすべて連結している必要があるため、６０階のような迷路は絶対に生成されません。

★S　TODの迷路生成で忘れていた条件判断がありました。

柱から壁を伸ばしたときに、現在生成中の壁、つまり自分自身に当たってしまう場合は、別のルートを選ぶ。というのがありました。「コの字」型のところに突っ込んだりした場合は、さらに１つ前に柱に戻ってやり直したような気がします。

--------------------------------

□　右手法、左手法で全体を巡回できるように

★B　まさに、これが可能なようにです。迷路に弱い人って、この方法に頼るしかないから。

上の書き方はアルゴリズムとして少しわかりにくいので私が以下に書きなおす。

【定義】

「壁つきの柱」とはその柱の上下左右のうち1箇所以上すでに壁がつけてある柱のこと。

「壁なしの柱」とはその柱の上下左右のうち壁がまだつけてない柱のこと。

1. 画面左上の柱から順番に調べていく。壁付きでない柱に対してだけ以下の2.～4.の処理をして壁を伸ばす。

2. いま注目している柱から壁を伸ばす。0～3の乱数により、それに相当する方向(0:上,1:右,2:下,3:左)に壁を作る。

3. 伸ばした壁が外壁か、壁つきの柱に到達したなら終了。

4. 0～2の乱数(0:進行方向左、1:まっすぐ、2:進行方向右)により、いま注目している柱から壁をさらに伸ばす。3.に戻り繰り返す。

参考動画として次の動画を挙げておく。
「FC版 ドルアーガの塔 FLOOR1 マップ生成手順」：http://youtu.be/kwey3y7jL7w

ただし、3.で伸ばすときに自分自身(上記2.～4.で処理中の柱)にはぶつからないようにという条件が必要のようだ。(ぶつかると閉ループが出来てしまう)

また「(3方向とも処理中の柱であったなら)一つ前の柱に戻ってやりなおしたような気がします」と遠藤さんはおっしゃっているのだが、一つ前の柱に戻っても下図のようになっていると何度やっても行き止まりになってしまう。

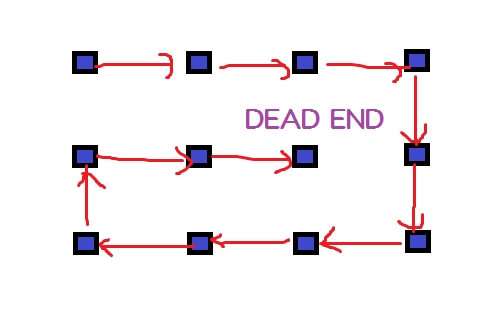
つまり、一つ前の柱に戻ってやりなおすという処理だとまずく、そういう処理はしていないと私は思うのだが、もしかするとたまたまそういう形の乱数は発生せず、うまく迷路生成が出来ているのかも知れない。

ただ、自分自身にぶつかった場合はその壁は作らずに処理を終了させる場合、その周囲に次図のように開ループが出来てしまうことがある。(緑の線で書いた経路)

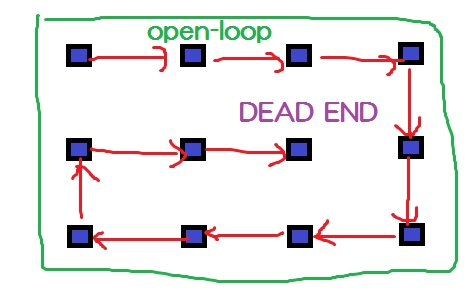
今回生成した壁すべてをキャンセルして、再度元の柱からやりなおすような処理にすれば良いのだが、生成しなおすのが馬鹿らしいので、生成中の柱による袋小路に突っ込んでしまった場合は、生成した壁は消さずにひとつ戻る。その柱の3方向が生成中の柱ならばさらにひとつ戻る。(以下繰り返し)

というように、生成した壁は消さずに柱をいくらでも戻っていくようなアルゴリズムになっている必要があると思う。

さて、このアルゴリズムで生成した迷路に開ループと閉ループが存在しないことを証明しなければならないが、この証明が結構やっかいなので簡単な説明だけをする。

それぞれの柱に着目した場合、その柱から伸びいている壁は1つに定まる。つまりこのアルゴリズムで迷路を生成した場合、柱の本数だけ壁が存在する。

なぜなら、上記1.で壁なしの柱から壁を伸ばしていき、どこかに当たった時点で停止するので棒倒しのように、壁にはそれに帰属する柱が定まるというわけだ。

また伸ばしていくときに自分自身には衝突しない(閉ループができない)ようにしている。

いま下図の赤い矢印が壁だとして、ここに緑の破線のような壁を作って閉ループが作れるかどうかを考えてみる。

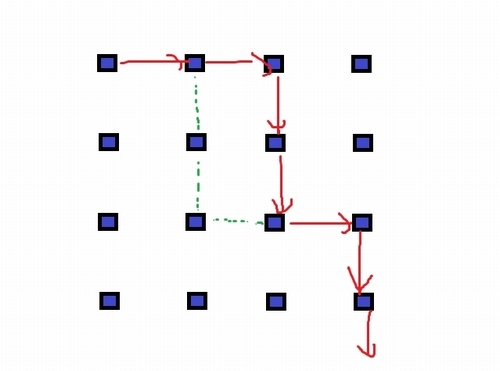
緑の破線の壁は3つであるが、棒倒しのように倒せる柱は2つしかない。つまり、閉ループになっていない柱と壁のつらなりに対して、このアルゴリズムでは閉ループが追加されることはない(倒せる柱の数が1つ足りないから)ことが保証されている。ゆえに閉ループは出来ない。

次に、開ループが出来ないことを証明しよう。たとえば1本の柱のまわりに開ループをつくるとする。以下図のようになるが、この中央の柱をどちらかに倒さなければならないので開ループにならない。(赤い矢印は壁で、ここが閉ループに見えますが、実際はどこかの壁が開いていると考えてください。この赤い壁による閉ループの内側では、ある二点に対して経路が複数あるのでこれは開ループになっていると言えます。)

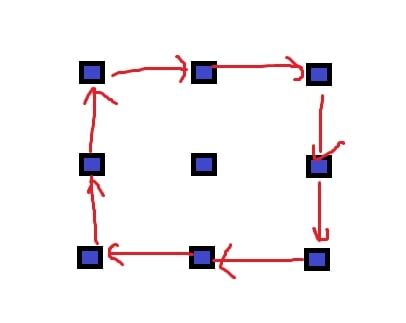
同様に下図の場合もまんなかの2本の柱をどのような組み合わせで倒しても開ループが壊れてしまう。

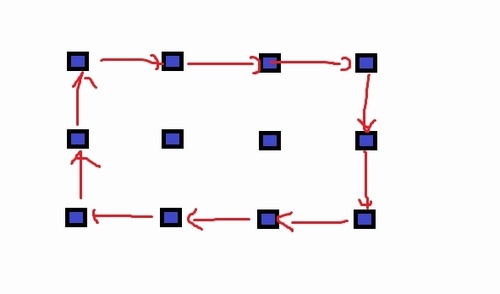
下図も同様。中央の4本で閉ループを作っていいのなら開ループが出来るのだが、閉ループを作れないことは証明済み。

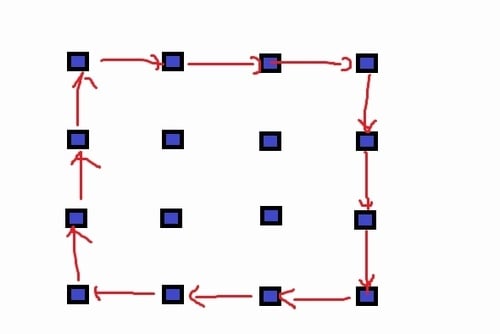
このように開ループを作ってもその内側にある柱から絶対に1つは壁が伸びてくるので開ループは出来ない。

迷路作成アルゴリズムには棒倒し法というのがあって(あまり質のいい迷路が出来るわけではないので取り上げなかった)、棒倒し法で閉ループ・開ループが作られないという証明は上記と同様にして出来るのではないかと思う。

ドルアーガの塔の迷路生成アルゴリズムで閉ループ・開ループが作られない証明が得られたので、次にドルアーガの塔のフロア60の話に移ろう。

遠藤さんの話を思い出そう。

　・フロア番号(1～60)を乱数のseedとして生成していた。

　・乱数のseedを255にすると「整然とした迷路になった」。これをフロア60に使うことにした。

あと、

　・乱数は線形合同法で生成している。

これは別のところで遠藤さんがおっしゃっていたと思う。

ドルアーガの塔 アーケード Floor 60

上図がフロア60である。もう棒がどちらに倒れているかは図示しなくてもおわかりだろう。すべて左に倒れている。すなわち、「0～3の乱数により、それに相当する方向(0:上,1:右,2:下,3:左)に壁を作る」ときに、3が出続けたというわけだ。

0～3の乱数なので発生させた乱数を4で割った余りだろう。

線形合同法は下位ビットの乱数としての精度が悪いことが多いのでビットシフトをしてまんなか付近のビットを取り出すこともあるが、たぶんそれはやってなくて、255をseedにして乱数を発生させ、下位2ビットを取り出すと3ばかりが出てきたのだろう。

線形合同法はもともと下位ビットの乱数としての精度は悪いのだが、当時の事情を考えると、それだけではない気がする。

ドルアーガの塔ではCPUはMotorola社のMC6809で動いていたからMUL(乗算)はあっても除算はなく、除算のルーチンは結構面倒なので除算せずにビットマスクで済ましてあったのではなかろうか。

すなわち、線形合同法の次式に対して、

線形合同法（せんけいごうどうほう、Linear congruential generators,LCGs）とは、擬似乱数列を生成するアルゴリズムの一つ。

漸化式

によって与えられる。A、B、Mは定数で、M>A、M>B、A>0、B>=0である。

Mを2のN乗にする。(こうすればビットマスクで済む)

MC6809のMULは8ビット×8ビットが16ビットで結果が得られる。(Aレジスタ×Bレジスタ = Dレジスタ)

MUL一回で求めようとすれば、上式のAは8ビット、Xnは前回の乱数(8ビット)になってしまい、乱数の周期が極めて短くなってしまう。さすがにこれは無いと思うのだが、ともかく、Xnの初期値がseedで、これが255だと、0～3の乱数を発生させたときに3ばかりが出続けたということのようだ。

あと、剰余を求めるコストが馬鹿にならなかったということで思い出したが、「0～2の乱数(0:進行方向左、1:まっすぐ、2:進行方向右)により、いま注目している柱から壁をさらに伸ばす。」という処理をするために0～2の乱数を発生させなければならないが、発生させた乱数を3で割った余りを求めるのは嫌なので、4で割った余り(これならビットマスクで得られる)を求め、それが3だったなら乱数発生からやりなおす、というような手法が取られることがある。

このとき、やりなおすのではなく、得られた数値が3だったなら1とみなすようにすれば、0と2が出る確率がそれぞれ25%で、1が出る確率が50%の乱数になる。ドルアーガの塔では、直進方向の壁を確率高めに生成したほうが迷路っぽくなると思うので、もしかしたらそういう処理になっているかも知れない。[要検証]

ともかく、ドルアーガの塔の迷路生成についての解説が一通り終わった。

上記のアルゴリズムは遠藤さんのオリジナルのようなのだが、現代でも十分通用する手法だと思う。

このアルゴリズムの優秀さに私は感心すると同時に、現在にこういった手法が受け継がれていないことを残念に思う。

迷路の自動作成の話題としては最近ではイラストを与えて、それを迷路化するのが流行っているようなのだが、これについて書こうと思っていたらすっかり出かける時間になってしまった。以下のサイトを紹介してこの記事を終わる。

「Maze Design」 『Craig S. Kaplan』

http://www.cgl.uwaterloo.ca/~csk/projects/mazes/

執筆： この記事はやねうらおさんのブログ『やねうらお－俺のブログがこんなによっちゃんイカなわけがない』からご寄稿いただきました。